前言

Dijkstra算法又称迪杰斯特拉算法，它采用的是一种贪心的策略，使用广度优先搜索的方式解决带权有向图或者无向图的单源最短路径问题，需要注意的是它不能处理带负边权的情况，核心思想就是“守住现有阵地不断攻占底盘”，这一点可以在后面代码实现中慢慢体会，接下来梳理一下算法思路。

Dijkstra思路

Dijkstra 算法的思路是维护一个点集合 S 和一个用来保存起点 m 到各个顶点到各个顶点最短距离的数组 dis，用邻接数组来表示带权图信息。

初始情况时，集合 S 中只包括起点m，通过图信息来初始化 dis 数组，将起点 m 可以直接到达的点设置为边的权值，不能到达的点设置为无穷大，比如点 m 到点 n 的距离是d，则 dis[n] = d。

然后从带权图中选择不在集合S 中的到点 m 距离最近的点，假设为 n，把它加到集合 S 中，然后尝试通过点 n “松弛” 那些不在集合 S 中的点到点 m的距离，更新 dis 数组信息，具体操作就是使用点 n 作为中转，如果距离如果点 m 到任意点 x 通过点 n 中转距离变短了，那么就更新 dis[x] 的值。

之后不断重复上面的“松弛”操作，直到集合 S 中包含了所有得到顶点，至此就通过Dijkstra算法求解出了从点 m 到图中任意点的最短距离。

图解实例

看了上面的关于Dijkstra算法的文字描述可能还是有点蒙，这时候需要画个图来解释一下，对于算法问题，特别是图论方面的算法题，有时候真的是一图胜千言，奈何我真的是不想画图，一方面因为“懒”，另一方面就是图片的搬运比较麻烦，所以对于大部分问题我都是文字描述，但是为了解释这个Dijkstra我还是决定画一画，假如求解从点a 到各个顶点的最短距离，初始图信息如下：

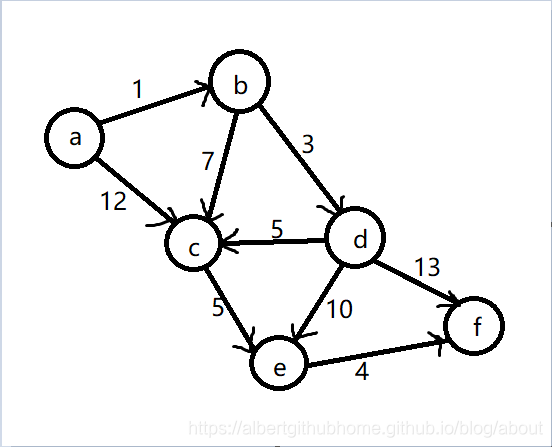
Dijkstra_0

第一步，我们把点 a 添加到集合 S 中变为 S = {a}，然后初始化dis数组为 dis = {0, 1, 12, ∞, ∞, ∞}，加入集合的点用红色表示，操作之后更新如下：

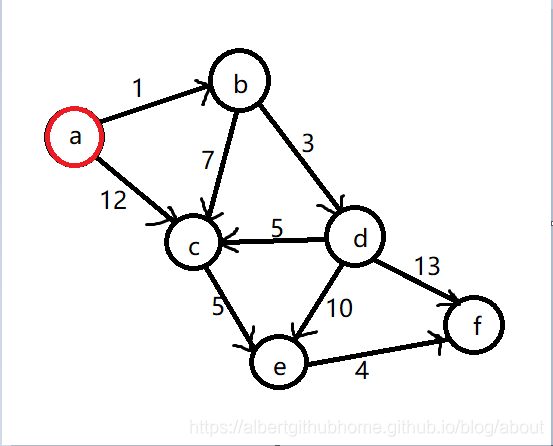
Dijkstra_1

第二步，找到距离点 a 最近的且不在 S 中的点，根据 dis 数组计算应该是点 b，将点 b 添加到集合 S 中，通过点 b 中转更新 dis 数组，dis[c]变为8，dis[d]变为4，更新后集合为 S = {a, b}，距离数组为 dis = {0, 1, 8, 4, ∞, ∞}, 图信息如下：

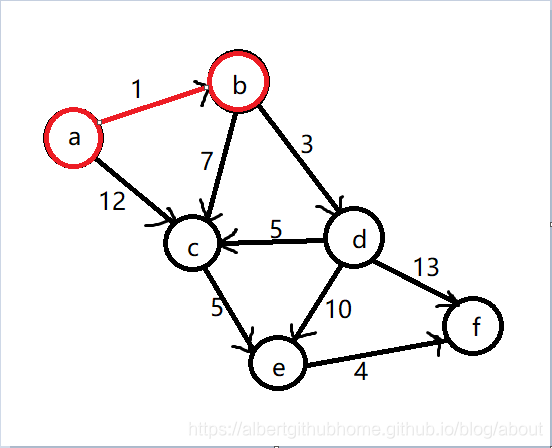
Dijkstra_2

第三步，找到距离点 a 最近的且不在 S 中的点，根据 dis 数组计算应该是点 d，将点 d 添加到集合 S 中，通过点 d 中转更新 dis 数组，dis[e]变为14，dis[f]变为17，更新后集合为 S = {a, b, d}，距离数组为 dis = {0, 1, 8, 4, 14, 17}, 图信息如下：

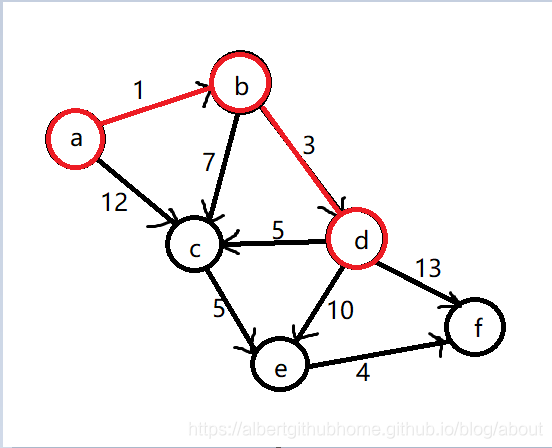
Dijkstra_3

第四步，找到距离点 a 最近的且不在 S 中的点，根据 dis 数组计算应该是点 c，将点 c 添加到集合 S 中，通过点 c 中转更新 dis 数组，dis[e]变为13，更新后集合为 S = {a, b, d, c}，距离数组为 dis = {0, 1, 8, 4, 13, 17}, 图信息如下：

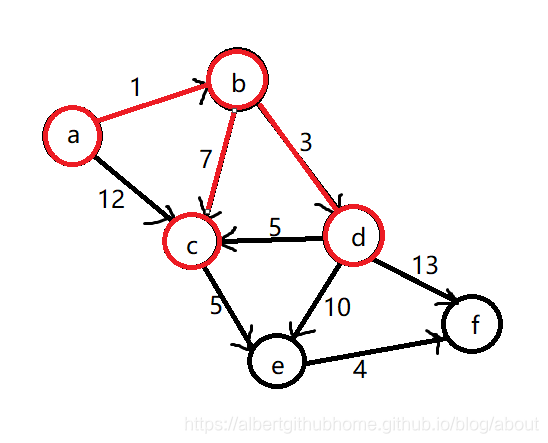
Dijkstra_4

第五步，找到距离点 a 最近的且不在 S 中的点，根据 dis 数组计算应该是点 e，将点 e 添加到集合 S 中，通过点 e 中转更新 dis 数组，通过距离判断发现此次不需要更新dis数组，更新后集合为 S = {a, b, d, c, e}，距离数组为 dis = {0, 1, 8, 4, 13, 17}, 图信息如下：

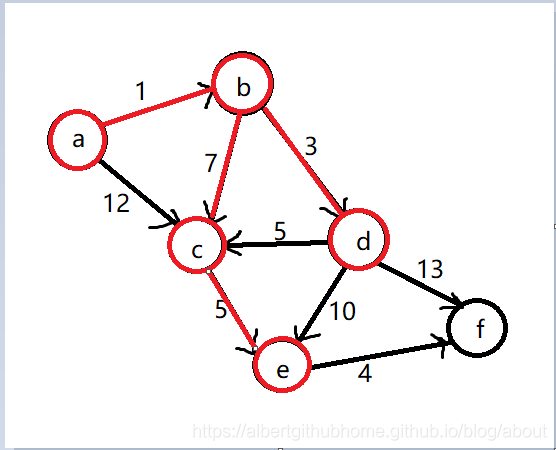
Dijkstra_5

第六步，找到距离点 a 最近的且不在 S 中的点，根据 dis 数组计算应该是点 f，将点 f 添加到集合 S 中，至此集合 S 中包含了所有的顶点，Dijkstra算法执行结束，集合信息为 S = {a, b, d, c, e, f}，距离数组为 dis = {0, 1, 8, 4, 13, 17}, 图信息如下：

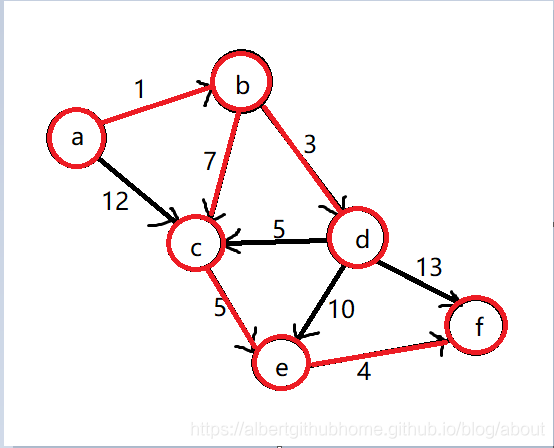
Dijkstra_6

代码实现

通过上面的图解实例对于Dijkstra的实现应该有了一些思路，那么接下来我们把它转化成代码：

void Dijkstra(vector<vector<int>>& graph)
{
    vector<int> dis = graph[0];
    set<int> S;

    const int n = dis.size();
    for (int i = 0, x = 0; i < n; i++, x = 0) {

        // find  minimum weight
        for (int j = 0; j < n; j++) if (!S.count(j) && (x == 0 || dis[j] < dis[x])) x = j;

        S.insert(x);

        // relax
        for (int j = 0; j < n; j++) if (!S.count(j) && dis[x] + graph[x][j] < dis[j]) dis[j] = dis[x] + graph[x][j];
    }
}

运行上述代码之后我们便得到了节点0到任意点的最短路径长度数组 dis。

从上面的分析我们可以知道从点 a 到点 f 的最短路径长度是 17，那么最短路径怎样求呢？

其实只要在做松弛操作时记录每个节点是从哪个节点松弛得到的就可以了，比如可以使用一个pre数组来记录这个信息，当计算 dis 结束时通过pre数组反推就可以得到最短路径，简单实现如下：

void Dijkstra(vector<vector<int>>& graph)
{
    vector<int> dis = graph[0];
    set<int> S;

    const int n = dis.size();
    vector<int> pre(n, 0); // save previous point index

    for (int i = 0, x = 0; i < n; i++, x = 0) {

        // find  minimum weight
        for (int j = 0; j < n; j++) if (!S.count(j) && (x == 0 || dis[j] < dis[x])) x = j;

        S.insert(x);

        // relax
        for (int j = 0; j < n; j++) if (!S.count(j) && dis[x] + graph[x][j] < dis[j]) {
            dis[j] = dis[x] + graph[x][j];
            pre[j] = x;
        }
    }

    // output path info
    vector<int> path{5};
    while(path.back() != 0) {
        path.push_back(pre[path.back()]);
    }

    for (auto it = path.rbegin(); it != path.rend(); it++)
        cout << *it << " ";
}

总结

Dijkstra算法的时间复杂度为O(N^2)，空间复杂度为 O(N)，如果对时间复杂度有更高要求可以使用堆结构进行优化
Dijkstra是一种求解单源最短路径的算法，在时间复杂度这一项要优于之前所说的 Floyd 算法
Dijkstra不能处理带负边权的情况，不过实际生活中类似于行车路线、管道铺设等问题都不会有负边权，应用还是比较广泛的
该算法仔细分析之后还是比较好理解的，不过还是有一些变型和编程技巧，需要在实际问题中灵活变通

==>> 反爬链接，请勿点击，原地爆炸，概不负责！<<==

历史总是惊人的相似，却不会简单的重复。在柯立芝实行了以放任自流的经济政策之后，紧接着便迎来了1929年的大萧条；而在克林顿到小布什任期内采取的经济自由化的政策，引发了之后2008年的国际金融危机；如今我们抬头看看大洋彼岸那疯狂运转的印钞机，这次的泡泡或许很快就能迎来炸裂的时刻~

2021-9-12 23:29:46