前言

Floyd-Warshall算法简记Floyd算法，又称弗洛伊德算法，是解决任意两点间的最短路径问题的一种常用算法，核心思想就是“不断利用第三者影响原配关系”，这一点在4行核心代码中表现的淋漓尽致，接下来梳理一下算法思路。

Floyd思路

从A点走到B点要想路径最短只有两种可能，一种就是直接从A到B，另一种就是通过其他点来中转，Floyd的思路就是先把直接能到达的点固定下来，然后不断的尝试从其他点来中转来降低路程。

Floyd算法实现通常使用一个二维数组来表示任意两点之间的初始距离，每个点到自身的距离为0，若两个点之间没有直接连通，则赋值为 +∞，我们假设这个二维数组是 v，则 v[i][j] 代表了从点 i 到点 j 的初始距离。

假设不允许中转，那么二维数组 v 中的数据就代表了任意两点间的距离。

如果允许中转一次，我们假设只允许从节点1进行中转，那么点 i 到点 j 的最近距离最小为 v[i][j] 或者 v[i][1] + v[1][j]，如果 v[i][1] + v[1][j] 的值更小，我们可以使用它来更新 v[i][j] 的值，这时 v[i][j] 就不仅仅是一个值了，而是隐含着 i->1->j 这样一条路径，这个过程实际上翻译成代码就是：

1
2
3

for(int i = 0; i < n; i++)
    for(int j = 0; j < n; j++)
        v[i][j] = min(v[i][j], v[i][1] + v[1][j]);

那么这条路径怎样才能更短呢？

答案就是引入另一个点，比如我们不仅允许从节点1中转，也允许从节点2中转，从上一步我们知道从从点 i 到点 j 的最短距离是从 i->1->j 得到的，实际上经过上面一步，任意两点的距离都是允许从节点1中转条件下的最小值，那么引入节点2之后就是要看看 v[i][j] 和 v[i][2] + v[2][j] 谁更小一点，然后遍历更新即可，类似的代码可以写成：

1
2
3

for(int i = 0; i < n; i++)
    for(int j = 0; j < n; j++)
        v[i][j] = min(v[i][j], v[i][2] + v[2][j]);

看到套路了没有，就是每个点都作为一个可能中转的点来试一下，整个算法就结束了，好神奇~ 完整4行代码如下：

for(int k = 0; k < n; k++)
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            v[i][j] = min(v[i][j], v[i][k] + v[k][j]);

简单粗暴又不失美感！

示例

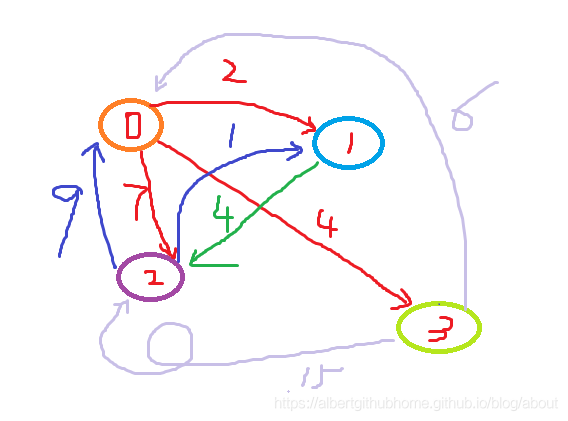
初始路径及每条边的距离如图：

翻译成二维数组如下：


0	2	7	4
∞	0	4	∞
9	1	0	∞
6	∞	15	0

仅通过节点0作为中转，二维数组更新如下：


0	2	7	4
∞	0	4	∞
9	1	0	13
6	8	13	0

增加节点1作为中转，二维数组更新如下：


0	2	6	4
∞	0	4	∞
9	1	0	13
6	8	12	0

再增加节点2作为中转，二维数组更新如下：


0	2	6	4
13	0	4	17
9	1	0	13
6	8	12	0

最后增加节点3作为中转，二维数组更新如下：


0	2	6	4
13	0	4	17
9	1	0	13
6	8	12	0

至此我们就求解出了任意两点间的最小距离。

总结

Floyd算法的时间复杂度为O(N^3)，空间复杂度为 O(N^2)
Floyd是一种求解多源最短路径的算法，如果是求解单源最短路径这 N^3 的时间复杂度确实有点伤
Floyd可以正确处理有向图或存在负权边的图，但不能处理存在负权回路的图的最短路径问题
4行代码3层循环或许可以助它称为最容易让人理解的最短路径算法
这4行代码只是一个理想化的模型，实际在编码时要注意加法的越界问题，因为两个无穷大相加理论上是无穷大，但在代码里可能就崩溃了

==>> 反爬链接，请勿点击，原地爆炸，概不负责！<<==

人生到底是追求到达目的地还是准备欣赏沿途的风景，一味地向前奔跑忽略了周围的一切，很多美好的事物就在身边却不自知，我们已经被世俗蒙蔽了双眼，什么时候可以慢下来呢？

2021-9-7 01:14:05