前言

进入正题之前先唠叨几句，不久前听到一个名词叫——费曼学习法，核心思想就是用通俗的话语把复杂道理或技术讲清楚，如果你已经明白了这个方法的含义，那么我好像离成功又进了一步。其实这个方法一直在尝试使用，但是没想到它居然有个“洋气”的名字。

由于之前学习时接触了加密、验证、HTTPS、证书等知识，感觉挺有意思的，最近也用到了一些这方面的内容，所以决定把这些概念重新梳理一下，免得一段时间不复习又还给书本了。本打算写一篇总结把这些概念整理到一起，但是初步想了一下很难实现，涉及到的概念实在太多了，所有还是决定分成几次来写吧。

分开写就比较随便了，写到哪完全看心情，不过我还是力图用最简单的描述来讲清楚问题，抛开具体的实现细节（其实我也不懂），梳理流程和概念性的知识，想了解具体的实现细节还是找专业的书籍去补充吧，我曾经看了一遍《图解密码技术》，过了这么久整本书我就记得两个词——异或、求余，再比如使用公钥和私钥来完成非对称加密，就是利用了两个大质数 (p,q) 乘积 (n) 难以逆向求解，这些太细节的东西很难展开一点点讲清楚。

最理想的状态是把学习知识当成是看故事书，阅读完一个个情节就吸收的差不多了，而不是把这些知识当成武功秘籍，然后一点点参悟，最后觉得枯燥而放弃，所以为了知识解惑，也算是将学习成果做个笔记，我们开始从最基础的知识学起。

对称加密

对称加密一般指：加密和解密使用的是同一个密钥的加密方式。就像防盗门的钥匙一样，可以用钥匙把门锁上，也可以用这同一把钥匙再把门打开。

对称加密示例

至于密钥怎么使用要看具体的加密算法了，可以举一个简单的例子，比如有下面这样一句话：

I like cat

我想把它发给一个好朋友，但是又不想被别人看到，万一有其他人一眼看到，那我的喜好就暴露了（那有怎样呢？），这时我们可以把这句话改的稍微隐晦一点，我可以和好友约定一个密码，假设是 1，然后我把原来这句话的每个非空白字母都替换一下，按字母表顺序使用后一个字母替换前一个字母，比如用字母 b 替换字母 a，那么这句话就变成了：

J mjlf dbu

这时就不怕被别人一眼看穿消息内容了，没有意义的字符串是比较难记的，但是当我的好友收到这句话时，使用我们约定的密码 1 就知道字母顺序变换了1位，所以他再将将字母反向替换回来就能够将文字还原。

这个例子很简单，但可以说明对称加密的关键，就是加密解密使用同一个密钥，例子中的 1 就是这个密钥，它可以让解密者知道，还原信息时需要反向移动1位即可，消息发送流程如下：

graph LR
A[I like cat] -- 用1加密 --> B((J mjlf dbu))
B((J mjlf dbu))-- 发送给好友 --> C((J mjlf dbu))
C((J mjlf dbu))-- 用1解密  --> D[I like cat]

对称加密的问题

刚才的例子已经说了对称加密的流程，但是有一个问题需要解决，这个密码 1 我要怎么告诉我的好友呢？直接发消息被别人看到怎么办，打电话也有可能被别人窃听啊！

密钥配送

这就涉及到了一个密钥配送的问题，如果想让对方解密就需要把密码发过去，但是密钥有可能被其他人窃取，这样秘密就不再是秘密了，可能你会想即使密码被别人窃取了也不要紧，因为他根本不知道怎么用。

请不要做这种假设，简单的情况没有密码都能破解，更何况在密码和数据都被窃取的情况下呢，另外在密码领域我们建议使用完全公开的密码算法，这样的算法经过时间的检验才能被用于加密，千万不要独创一套自认为很安全的加密算法，单靠隐藏算法的细节来达到加密的目的是很危险的。

发送密钥可能被窃取，不发送密钥对方无法解密，这个加密的密钥配送问题是使用对称加密必须要解决的，而下面要说的这种非对称就不同了，可以将一把密钥直接发送给对方，即使被窃取也没有关系。

非对称加密

看这个名字就知道它有点“针对”那个叫做对称加密的小伙伴，从定义上来说对称加密指的是加密和解密使用相同的密钥（为啥不叫同钥加密咧），而非对称加密指的是加密和解密过程使用不同的密钥来进行。

乍一听好像有点不可思议啊，怎么滴，难道还能两把不同的钥匙开一把锁？确实可以！这有点像中学物理里面的两个开关控制一个灯泡。在一个漆黑的楼梯两端，分别有一个开关，控制着楼梯上方的一个灯泡，上楼前先打开楼梯下面的开关，然后上楼后关掉楼梯上面的开关，而下楼时进行相反的操作，先打开楼梯上面的开关，然后下楼后默认楼梯下面的开关，找了张电路图，感兴趣可以再分析一下。

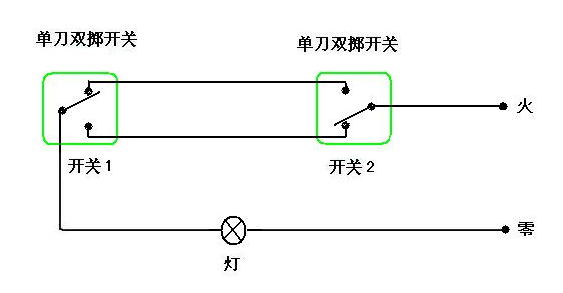
单刀双掷开关

不过非对称加密和这种双掷开关不完全相同，使用开关时可以在同一端打开或关闭，但是非对称加密时，只能在一端加密，然后在另一端解密，同一端是不能同时加密和解密的。

公钥与私钥

具体地，非对称加密指的是根据特殊规则生成两把密钥 A 和 B，分别叫做公钥和私钥。私钥自己保留，公钥则分发给自己的小伙伴用来用来和自己通信，理论上生成的两把密钥选择哪一把作为私钥都可以，但是出于效率和安全等方面的要求，公钥和私钥再生成时会给出特殊的条件，所以在实际使用过程中，两者通常是不会互换的。

非对称加密的示例

使用公钥和私钥怎样完成非对称加密呢？下面来看一个具体的场景，比如有 Tom 、Jerry 、Spike 三个小伙伴，有一天 Jerry 想给 Tom 发点小秘密，又不想让 Spike 发现，首先他想到的是对称加密，先和 Tom 约定一个密码，再给 Tom 发送加密消息，但是想到前几天，自己和 Tom 的消息被 Spike 破解了，因为两个人发送密钥和加密消息的过程都被窃听了，如果这次的消息再被窃听到怎么办？

后来Jerry想起Tom曾经自己生成了一对公钥和私钥，然后把公钥发给了自己和 Spike，那这样就可以使用非对称加密了，Jerry 使用 Tom 给的公钥把要发送的小秘密进行加密，然后发送给了 Tom。这时 Spike 果然在窃听，但是窃听到的消息使用了 Tom 的公钥进行了加密，只有 Tom 拥有解开这条消息的私钥，而 Spike 虽然拥有 Tom 的公钥也是解不开的。

graph LR
A[I like cat] -- Jerry用Tom公钥加密 --> B((密文))
B((密文))-- 发送给Tom --> C((密文))
C((密文))-- Tom用自己的私钥解密  --> D[I like cat]

怎么判断解开

上面的描述中出现了“解开”一词，这两个字在我刚开始学习加密这些知识的时候困扰了我好久，查了好多讲解也没弄明白，什么叫能解开，什么叫解不开。它不像现实生活中的事物那么形象，比如把电视打开，那么电视就出现图像了，把锁解开门就能打开了。在数据加密的过程中，数据本质上是一堆二进制数据，加密之后还是一堆二进制数据，解密时使用密钥进行特定的运算就会得到解密后的二进制数据，怎么判定这些“解开”的数据是否是原数据呢？

后来在不断的学习过程中，接触了一些开源的非对称加密算法实现，比如常用的 RSA，基础的函数包括公钥加密、私钥解密、私钥加密、公钥解密等，当你在解密时将密文和密钥传入解密函数进行特定的运算，计算过程和计算结果必须满足特定的条件，这些条件是算法保证的，如果有条件不满足那么解密失败，这就是上面所提到的解不开。

非对称加密的问题

之前提到对称加密时，密钥配送问题是一个难题，因为网络上发送密钥很容易被截获，无法保证密钥不被窃取。很多情况下又不能面对面的传递密钥，而非对称加密的出现解决了这个问题，因为公钥是可以被任何人知道的，所以网络上发送公钥就不怕被窃取，但是如果例子中，Jerry 收到的 Tom 的公钥实际上在途中被 Spike 替换了怎么办？

这就又引入了一个问题——中间人攻击，形象的来表述就是有第三方 Spike 侵入了原本两个人 Tom 和 Jerry 的通信中，Spike 对 Tom 时把自己伪装成 Jerry，和 Jerry 沟通时又将自己伪装成 Tom，这样原本两个人的沟通信息全都被第三方窃取了，这个问题的根本就是获取公钥不可信，不过证书中心可以解决这个问题，后面我们再继续深入了解，这里就不展开了。

对称加密和非对称加密对比

加密类型	常见算法	加密处理速度	遇到的问题	解决办法
对称加密	DES、AES	快	密钥配送问题	面对面交换或者使用非对称加密传送秘密
非对称加密	RSA、DSA	慢	中间人攻击问题	通过证书中心来解决中间人攻击

总结

虽然想写的尽可能的通俗易懂，但还是不免会引入一些令人犯困的概念，一开始记住就好，后面理解了不会觉得枯燥
还在不断尝试表达方式，总结中融入了一些我当时学习时的想法和疑惑，我遇到的这些问题应该很多人也遇到过
使用对称加密方法，速度快，效率高，但是会面临密钥配送的问题
非对称加密虽然很巧妙的，但是效率较低，所以一般的用法是使用非对称加密来传送简短的对称加密密钥，然后再使用对称加密的方式传送数据
为了更好的加密你的数据，应使用公开的加密算法，他们都是经过时间考验的，单靠隐藏加密细节来加密时很危险的

==>> 反爬链接，请勿点击，原地爆炸，概不负责！<<==

见过了外面的大千世界，便不再甘心留在原地，而这种不甘心恰恰就是动力~